Chu vi hình tròn là một trong những khái niệm nền tảng nhất của hình học phẳng mà học sinh nào cũng gặp từ sớm. Khi hiểu rõ bản chất của đại lượng này, bạn sẽ biết cách đo độ “dài” của đường tròn bao quanh một hình tròn. Trong thực tế, kiến thức này giúp ước lượng vật liệu làm viền tròn, tính quãng đường đi quanh bồn hoa, hay kiểm tra kích thước bánh xe. Bài viết dưới đây trình bày công thức, cách tính, ví dụ, cùng các mẹo ghi nhớ để bạn vận dụng chính xác và nhanh chóng.
Chu vi hình tròn là gì?
Định nghĩa dễ hiểu
Trong hình học, chu vi là độ dài đường bao quanh một hình. Với đường tròn, đó là tổng chiều dài “vòng tròn” ôm lấy vùng bên trong. Vì là đường cong khép kín, độ dài này được xác định thông qua hằng số pi (π) cùng các yếu tố đặc trưng của hình tròn như bán kính và đường kính. Khi nắm chắc các yếu tố này, bạn sẽ chuyển đổi linh hoạt giữa nhiều cách tính khác nhau.
Ký hiệu và các đại lượng liên quan
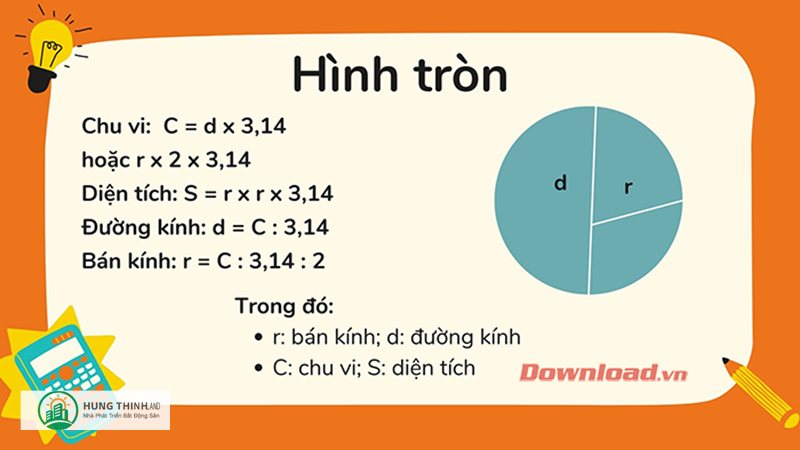
Quy ước thường dùng ký hiệu C cho chu vi, r cho bán kính, d cho đường kính và π xấp xỉ 3,14159 (hoặc 22/7 khi cần ước lượng nhanh). Mối liên hệ giữa các đại lượng là d = 2r, vì đường kính gấp đôi bán kính. Nhờ mối liên hệ này, công thức tính có thể viết dưới hai dạng tương đương, giúp bạn chọn cách phù hợp với dữ kiện bài toán.
Công thức chuẩn cần nhớ
Công thức cơ bản là:
- C = 2πr (tính theo bán kính)
- C = πd (tính theo đường kính)
Hai công thức này hoàn toàn tương đương vì d = 2r. Khi đọc đề, hãy xác định dữ kiện cho trước để thay thế đúng và tính nhanh.
Chu vi hình tròn trong đo lường thực tế
Chọn đơn vị và chuyển đổi
Trong các bài toán và ứng dụng đời sống, đơn vị đo phổ biến là milimét (mm), xentimét (cm), mét (m) hoặc kilômét (km). Khi dữ liệu lẫn lộn đơn vị, bạn nên quy đổi về cùng một hệ để tránh sai số. Ví dụ, nếu bán kính tính bằng cm thì chu vi cũng nên biểu diễn bằng cm để kết quả mạch lạc và dễ so sánh.
Độ chính xác khi dùng π

Tùy mục đích, bạn có thể dùng π ≈ 3,14, π ≈ 22/7 hoặc giữ π ở dạng ký hiệu để đến bước cuối mới làm tròn. Trong thi cử hoặc tính toán kỹ thuật, nên ghi kết quả với số chữ số thập phân theo yêu cầu đề bài. Việc làm tròn quá sớm có thể khiến đáp số lệch đáng kể, đặc biệt ở các bài toán có số đo lớn.
Lựa chọn công thức nhanh
Nếu đề cho đường kính, hãy dùng C = πd để rút gọn thao tác. Ngược lại, nếu đề cho bán kính, C = 2πr là tối ưu. Kỹ năng nhận dạng dữ kiện và “ghép” đúng công thức sẽ giúp bạn hạn chế sai sót và tiết kiệm thời gian làm bài.
Chu vi hình tròn: ví dụ minh họa
Ví dụ 1: Tính theo bán kính
Cho một hình tròn có bán kính r = 7 cm. Áp dụng C = 2πr, ta có C = 2 × π × 7 = 14π cm. Nếu dùng π ≈ 22/7, thì C ≈ 14 × 22/7 = 44 cm. Đây là trường hợp kinh điển vì r = 7 cm giúp tính nhẩm với 22/7 rất gọn, phù hợp khi cần ra đáp số nguyên.
Ví dụ 2: Tính theo đường kính

Một nắp cống tròn có đường kính d = 1,2 m. Áp dụng C = πd, suy ra C = π × 1,2 ≈ 3,7699 m nếu dùng π ≈ 3,14159. Trong thực tế, có thể làm tròn đến 3,77 m tùy mức chính xác mong muốn. Lưu ý giữ đơn vị mét để thống nhất với số đo đầu vào.
Ví dụ 3: Từ chu vi suy ra bán kính
Giả sử chu vi hình tròn của một vành xe là C = 2,2 m. Dùng C = 2πr, suy ra r = C / (2π) ≈ 2,2 / (2 × 3,14159) ≈ 0,35 m. Khi đề bài yêu cầu “tính ngược”, bạn chỉ cần biến đổi công thức một cách có hệ thống để tìm đại lượng còn lại.
Sai lầm thường gặp và cách khắc phục
Nhầm giữa diện tích và chu vi
Một lỗi hay gặp là dùng công thức diện tích S = πr² để tính chu vi hình tròn. Hai đại lượng này khác nhau về bản chất: chu vi đo “độ dài” đường biên, còn diện tích đo “độ rộng” vùng bên trong. Khi làm bài, hãy luôn đọc kỹ yêu cầu để chọn công thức đúng.
Quên đổi đơn vị hoặc đổi sai
Nếu bán kính tính bằng mm mà kết quả lại ghi bằng cm thì đáp số sẽ sai. Hãy thiết lập thói quen “chuẩn hóa đơn vị” trước khi thay số. Bạn có thể viết một dòng nháp quy đổi, ví dụ 10 mm = 1 cm, để tránh nhầm lẫn trong các bài nhiều bước.
Làm tròn quá sớm
Nên giữ π ở dạng ký hiệu trong các bước trung gian, chỉ làm tròn ở bước cuối. Cách này giúp hạn chế cộng dồn sai số, đặc biệt khi bài toán yêu cầu so sánh nhiều giá trị hoặc lồng ghép vào các phép tính khác.
Mẹo nhớ nhanh và vận dụng hiệu quả
Mẹo nhớ công thức
Hãy liên tưởng “đường kính đi với π một lần” (C = πd) và “bán kính đi với π hai lần” (C = 2πr). Một câu vần dễ thuộc là: “Đường kính nhân pi ra ngay chu vi; bán kính nhân hai, pi vào là đủ.” Sự vần điệu giúp khắc sâu công thức khi làm bài dưới áp lực thời gian.
Kỹ thuật kiểm tra nhanh
Sau khi tính xong, hãy ước lượng xem kết quả có hợp lý không. Nếu r ≈ 10 cm, thì chu vi hình tròn khoảng 2 × 3,14 × 10 ≈ 62,8 cm. Nếu bài làm ra con số 600 cm, khả năng bạn đã nhân nhầm một bậc. Việc “soi” nhanh bằng xấp xỉ giúp phát hiện lỗi ngay tại chỗ.
Gắn với tình huống thực tế
Hãy thử đo chu vi của nắp lon, miệng ly, hoặc vòng tay bằng sợi dây rồi so sánh với tính toán từ bán kính/đường kính đo được. Những trải nghiệm nhỏ như vậy khiến kiến thức trở nên sống động và dễ nhớ hơn nhiều so với học thuộc lòng khô khan.
Bài tập luyện tập
Bài tập 1
Một chiếc đồng hồ treo tường có bán kính 12,5 cm. Tính chu vi hình tròn của đồng hồ theo π và theo số thập phân làm tròn đến 2 chữ số. Gợi ý: C = 2πr; thay r = 12,5 và thực hiện hai cách trình bày.
Bài tập 2
Vành bánh xe đạp có đường kính 0,7 m. Tính chu vi hình tròn và ước lượng số vòng quay cần thiết để đi được 100 m trên đường thẳng (bỏ qua trượt). Gợi ý: số vòng ≈ quãng đường / chu vi.
Bài tập 3
Biết chu vi hình tròn là 31,4 cm. Hãy tìm bán kính và đường kính của hình tròn, làm tròn đến 1 chữ số thập phân. Gợi ý: r = C/(2π), d = 2r; dùng π ≈ 3,14 để thuận tiện tính nhẩm cùng hungthinhland
Kết luận và gợi ý học tập
Khi nắm vững công thức và cách đổi đơn vị, bạn có thể tính chu vi hình tròn nhanh, chính xác và ứng dụng được trong nhiều tình huống thực tế. Hãy luyện thói quen đọc kỹ dữ kiện, chọn công thức tương ứng và chỉ làm tròn ở bước cuối. Việc thực hành thêm bằng các ví dụ đời sống sẽ giúp bạn ghi nhớ lâu, tự tin hơn trong kiểm tra và thi cử. Nếu tiếp tục học sâu về hình tròn, bạn có thể mở rộng sang diện tích, cung – dây – tiếp tuyến và các bài toán liên hệ giữa góc – cung để hoàn thiện bức tranh kiến thức.
